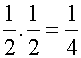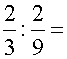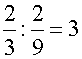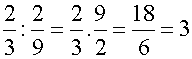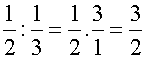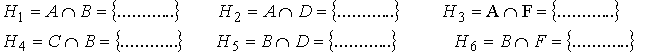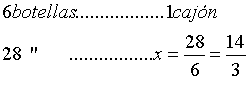Profesora María Luz Silva *

PROLOGO

La matemática siempre aparece como muy difícil de aprender. Muchos alumnos fracasan y otros la aprenden sin llegar a tener verdadero gusto por ella. Y pareciera ser que está reservada para un grupo exclusivo.

Durante años en una constante búsqueda y superación de mi propia didáctica para hacer más accesibles los conocimientos, partiendo no solamente de la posibilidad de aumentar mis conocimientos académicos sino del análisis de las propuestas que se presentan a los alumnos y cómo son elaboradas por éstos, el intercambio y acuerdos con equipos de trabajo, se fueron perfilando algunas hipótesis que se tradujeron en algunas experiencias áulicas que se presentan en forma general en este trabajo

Desde el punto de vista técnico todas las propuestas que presentamos fueron probadas a través de distintas experiencias en las que colaboraron varios docentes. Pero no se trata de una investigación sistemática.. En este sentido es que puede considerarse como una teoría a comprobar.

Los mayores logros se obtuvieron siempre que se trabajó en equipos, de docentes para analizar la realidad, de alumnos para aprender compartiendo. Por ello primero deseo agradecer a todos mis compañeros docentes que en alguna ocasión tomaron y ejecutaron algunas ideas, y generalmente las mejoraron con su aporte, y a todos mis alumnos que año a año me presentan el desafío de mantener el asombro, la curiosidad, la búsqueda, con sus individualidades irrepetibles.

La práctica docente implica un compromiso personal con el alumno y con la comunidad. Compromiso que existe a pesar de las situaciones coyunturales, donde muchas veces, la tarea del educador es exaltada a nivel del discurso político y desjerarquizada en las acciones concretas o en las políticas que se ponen en marcha.

El maestro, el profesor son la cara visible del Sistema Educativo, al que se ama u odia, al que se recordará o se olvidará, con quien se convive. Por eso, ningún educador puede permitirse dejar de crecer. Y se deja de crecer cuando se asumen conductas obsecuentes, cuando se queda atrapado en la rutina, cuando sólo se compite y no se comparte, cuando permite que las limitaciones materiales pongan freno a nuestra libertad interior, a nuestra capacidad creadora.

Si año tras año obtenemos los mejores logros con aquellos alumnos que aprenden con cualquier maestro o a pesar del maestro, entonces podemos estar seguro de que nuestra labor es intrascendente. Si, en cambio, ponemos nuestro conocimiento al servicio de la realidad para superarla, mantendremos viva la llama que invita a crecer.

Estas reflexiones no son una panacea, ni una receta, es una invitación a crecer:

- un sí al profesionalismo que incluye la formación del propio estilo didáctico en función de una constante actitud crítica y autocrítica

- un no, al individualismo, que promueva el trabajo compartido entre pares para generar el espacio para aprender más, aprender con el otro, para permitirse equivocase y corregirse en la conciencia de que todos podemos mojar y perfeccionar cualquier buena labor

- un sí, a la humanización que implica ejercitar los valores que no existen si no hay personas que los recreen

No está todo dicho. No está todo descubierto. No está todo hecho. El resto de su historia, mi historia, y la de los chicos que le son confiados en este tiempo aún está por escribirse

María Luz Silva

ENSEÑAR - APRENDER

La organización del Sistema Educativo, su reestructuración, constituyen un diseño formal que, a partir del análisis de la realidad y en función de condiciones finales ideales, determina los objetivos del sistema y establece, in abstracto, los medios idóneos para alcanzarlos. La implementación del diseño, quedará siempre limitada por la inversión monetaria que se realice, por la calidad de los recursos humanos y por la capacidad del sistema de autorregularse en el tiempo adecuándose a las demandas de la realidad.

No obstante ello, en general, son los ejecutores del sistema, es decir, los docentes quienes quedan identificados como responsables visibles del fracaso del planeamiento. Ellos a su vez, condiciones por la realidad, trasladan su responsabilidad a la familia, a la macroeconomía y al mismo sistema.

La calidad y la eficacia de la ejecución de todo planeamiento que involucre personas, como en el caso del Sistema Educativo, dependerá de las cualidades de los vínculos que se establezcan en función de los objetivos comunes a los que se adhiera, más que de la eficiencia individual de los actores y de los medios que se dispongan, sin embargo, se debe tener en cuenta que, la relación vincular no es independiente de la organización que se postule.

El Servicio Educativo se concretiza en el aula: lugar de encuentro entre personas La cualidad de los vínculos que se establecen no dependen solamente de la calidad profesional y humana del líder, sino que está influenciada por las estructuras institucionales, la forma en que se ejecutan los objetivos del sistema y el nivel de participación del docente en la toma de decisiones

Existen diversas variables a considerar. El rol del educador, por ejemplo, varia entre el servicio privado y el público. En el primer caso es el profesional que se contrata para llevar a cabo un proyecto curricular ofertado de antemano; en la escuela pública, en cambio, los limites a la libertad de cátedra y de acción están sólo regulados por las leyes y la unidad institucional, en cuyo planeamiento la misma legislación otorga al docente participación activa Asimismo, existe una diferencia cualitativa entre los receptores de tos servicios: En la escuela Privada, el receptor, al contratar la oferta, elige la forma en que ejerce su derecho constitucional a la educación; en la escuela pública es receptor del sistema reglado. Por lo tanto, la escuela pública deberá generar las condiciones para resguardar los mismos derechos aludidos. SÍ la prestación es precaria o meramente asistencia!, no resguarda la igualdad de oportunidades. El rol del educador y su protagonismo en la eficacia de la prestación del servicio educativo, exige mayor profesionalismo y compromiso allí dónde la escuela es el único medio de promoción social y cultural y, dónde los medios son menores. Es, en este entorno, donde la red vincular adquiere particular importancia y el nivel de profesionalismo requerido es mayor, en virtud de que, al liderazgo impuesto (característico de todos los estamentos del S.E), el logro de los fines, le exige aplicación de estrategias profesionales, no necesariamente imprescindibles a los líderes naturales.

El sistema puede limitar el profesionalismo cuando legisla sobre cuestiones sujetas a criterio, imponiendo metodologías o propuestas inaplicables, o promoviendo comentes ideológicas como panaceas de solución. Los estamentos de planeamiento tienen la atribución de establecer cambios, pero cuando ellos se imponen o los resultados se miden en comparación con las predicciones iniciales, sin atender a las variables de la realidad, y a las personas, si la norma supera el criterio táctico, el sistema corre el riesgo de producir su propio deterioro.

Cuando el sistema es autoritario, puede desembocar en situaciones de conflicto que, oponen la imposibilidad a la obligatoriedad, y da como resultado la adaptación a la forma, sin producir modificaciones de fondo, generando además de conductas alienantes, la corrupción de los valores y el descrédito de cualquier norma sin determinar fácticamente su competencia. El conflicto, que genera cualquier propuesta de cambio si como crisis entre lo que es y lo que debe ser, y se encara como problema a resolver, impulsa a la persona hacia su superación individual y al grupo a su crecimiento. Es función de los estamentos de conducción del Sistema, implementar tos cambios de modo que, en tos ejecutores, se genere el estimulo para la participación y recreación de las propuestas. Cada Servicio Educativo, en este enfoque, debería actuar en dos sentidos: ejecutando las misiones y funciones delgadas y aportando a los

subsistemas de planeamiento los datos de la realidad que permitan regular , actualizar o modificar las normativas referidas al macroplaneamiento.

Ahora bien. la retroalimentación del sistema exige calidad de ejecución, conducta ética y capacidad critica. Como Oscar Blake señala, "... una persona se desempeña profesionalmente cuando tiene determinadas sus áreas de competencias, conoce sus zonas de debilidad y actúa sobre ellas, utiliza adecuadamente el tiempo, usa métodos e instrumentos idóneos para cada circunstancia, se mantiene actualizado y se relaciona fluidamente con su grupo profesional, desarrolla una ética personal y profesional"

La tarea especifica del docente son educar. Para esta labor es insuficiente el voluntarismo, requiere una constante reflexión critica que incluye, no sólo la autocrítica sino el análisis de los mandatos, donde la obediencia obsecuente no tiene lugar. "En educación no hay conductas neutras", por acción u omisión, por impotencia o negligencia, se afianza una u otra ideología. En este sentido, existe cierta actitud a aceptar que determinados sectores de la población deben condenarse a un mediocre nivel de educación, a una asistencialidad que, en realidad, no les reconoce plenamente su dignidad humana.

El rol del docente en el proceso de enseñanza aprendizaje ha sido objeto de estudio , se ha oscilado a través del tiempo entre

Maestro - CONTENIDO - alumno, en la época del enciclopedismo y,

Maestro - contenido - ALUMNO, en la época del construccionismo

En cualquiera de ambas concepciones existe una estructura de concepción mecanicista - (recuérdese que el modelo es el mecanismo) - donde esas partes se unen para formar el todo, pero que se analizaban en forma separada. Para mostrar y destacar la unidad del proceso, se acuño la palabra "enseñaje", pero trasladado a la realidad, en pro de un construccionismo a ultranza se ha deteriorado el proceso mismo.

Por ello postulamos una concepción sistémica - (donde el modelo es el organismo) - para el proceso de enseñanza - aprendizaje:

Dos subsistemas independientes e interrelacionados:

§ La independencia establece las operaciones propias de cada subsistema, al interrelación involucra a las funciones de cada uno que afecta al otro subsistema, o que existen derivadas de este.

§ El sistema enseñanza - aprendizaje actúa sobre el contenido - en sentido amplio - que es lo que da razón de ser al sistema, que define las funciones de cada subsistema

Cuando el centro del proceso enseñanza-aprendizaje es el alumno interactuando con el objeto de conocimiento el rol del docente cambia: el expositor verbalista da lugar a un conductor que orienta y coordina la búsqueda y adquisición del conocimiento. Fuera del centro del proceso, el docente podría aparecer como el segundo actor que completa el cuadro, con responsabilidad indirecta en los logros, ya que, elegidos los medios adecuados, aquellos dependerían de la calidad de la interacción, más que de la intencionalidad del conductor

En líneas generales esa premisa es cierta: dos sujetos frente al mismo objeto de aprendizaje, en las mismas circunstancias, pueden variar cualitativamente el nivel de aprehensión. Sin embargo, si profundizamos el análisis podremos establecer algunas variables:

- El acento puesto en los multimedios, parecería indicar que los instrumentos atractivos son el modo de despertar el interés. Sin embargo, seria falaz considerar que no puede despertarse el interés del educando sin medios materiales de atracción. Es indudable que, si los alumnos no tienen acceso a instrumentos que requieren entrenamiento psicomotriz para su uso, (ej. pelota, regla, compás, computadora, etc.), no podrán adquirir habilidades especificas hasta tanto no realicen la práctica adecuada, por lo tanto, en estos casos el instrumento es imprescindible. No obstante, en general, las técnicas de interacción no tienen como condición necesaria, la posesión previa de un elemento único destinado a ese fin. Suponer, por ejemplo, imposibilidad de desarrollar un aula taller, si los alumnos no poseen los libro -cuadernos en boga (donde el consumidor compra, a precios increíblemente altos, una gran cantidad de papel en blanco), es admitir la incapacidad para aplicar una técnica sin la apoyatura del pensamiento de otro.

- Otra cuestión que debe considerarse es si habiendo despertado el interés exógeno, alcanza para promover la perseverancia, la curiosidad, la continuidad del propio desarrollo. En general, la respuesta a esta cuestión es negativa: Si la persona no está movilizada por un interés endógeno, el estimulo externo pierde eficacia y no hay garantía de retroalimentación que conduzca a la búsqueda de la educación permanente. La pregunta es cómo generar el interés endógeno, (ese disfrutar de " pararse en la propia cabeza"), y si su logro es función de los que hemos designado subsistema enseñanza.

En educación no existen posturas "asépticas de ideologías". Toda acción docente incluye una concepción, explicitada o no, de qué es la educación, el hombre, el mundo. Desde ese segundo plano que, aparentemente, adquiere el docente, ¿no es lógico considerar que, si las condiciones iniciales no son buenas, el proceso de enseñanza aprendizaje se mantendrá en nivel bajo?; ¿no es lógico esperar resultados mediocres en determinados grupos de alumnos que, por su marginalidad o sin ser marginales, posean deficiencias socioculturales previas?. Si esto fuese cierto la escuela debería declararse a si misma impotente e inservible para educar.

Este puede parecer un planteo extremista. Alguno puede escandalizarse y decir "nadie piensa eso". Sin embargo, no son producto de mi imaginaciones expresiones como:

-"En la escuela A, del centro, turno mañana, yo hago lo mismo que en la escuela B , del suburbio, turno vespertino, soy la misma persona, pero los chicos de la escuela A se eximen casi todos y en cambio, los de la escuela B se van casi todos a examen"

-"Imposible mejorar el nivel de estos chicos, no compran libros, no tienen material, y no estudian en la casa"

-"Si la familia no estimula, qué puedo hacer yo"

Detrás de cada expresión de esta naturaleza, existe ciertamente una realidad que incide negativamente sobre la adquisición de los contenidos, plantean un problema, y ese problema, la mayoría de las veces tiene solución. Probablemente no soluciones individuales sino las que requieren trabajo institucional, acuerdo entre pares, que priorice el desarrollo integral del niño que está frente a mí, en este momento y que tiene el derecho - cualquiera sea su origen - de educarse e instruirse. Identificar problema con imposibilidad, permite declararse incompetente para modificar situaciones iniciales adversas, desligar toda responsabilidad y favorecer, sin culpa, la discriminación por el origen, promoviendo acciones asistencialistas que no presentan al niño la meta de superarse a sí mismo

La tarea del docente es enseñar. Dependen de él, la elección de tos modos de abordaje de los objetos de conocimiento, y le corresponde la enseñanza de aquellos elementos - de las áreas del conocimiento- que el alumno no puede aprender por si mismo.

Lo que no debemos confundir es la "tarea de enseñar" con la "exposición verbalista". Se trata de la presentación de situaciones didácticas dónde la adquisición de lo especifico de cada ciencia o disciplina, integre relaciones y dé continuidad a la experiencia de aprendizaje. La construcción de un conocimiento especifico que el alumno efectivice en el proceso de enseñanza aprendizaje debe estar ligada, - pero no limitada - a las estructuras cognitivas, estrategias o habilidades, que debe desarrollar, referidas a los modos de conocer en el ámbito de ese conocimiento específico. La elección de los medios que cumplan esta función compete a la tarea de enseñar.

En su aspecto instrumental, la educación introduce al individuo en el conocimiento de la cultura de su tiempo. En todas las áreas del conocimiento producido por el hombre, existen códigos, vocabulario especifico y métodos que deben ser enseñados, sin perjuicio de las inferencias con que se logre la aprehensión del objeto.

Ejemplifiquemos: En una clase de laboratorio, los alumnos han pesado volúmenes distintos de una sustancia. A partir de la actividad guiada, han descubierto la constante de proporcionalidad. Luego construyeron tablas de proporcionalidad de varias sustancias. A partir de éstas, detectaron la sustancia de una muestra propuesta.

En este momento el docente debe enseñar cómo se define el peso especifico. De este modo, clasifica la experiencia, nombra el concepto adquirido en el lenguaje de la ciencia y da sentido a la acción en función de las próximas experiencias. De no hacerlo el concepto adquirido se transforma en un saber difuso, cuando no inservible.

En el aula, la tarea de aprender corresponde al alumno. Es posible - deseable y necesario- que el maestro también realice aprendizajes, porque como ser humano perfectible, su propio desarrollo depende de la revitalización de su universo personal y profesional. Pero en el aula, el objeto de aprendizaje está definido: El maestro no va a aprenderlo, sino a enseñarlo Planteada la situación didáctica, la adquisición del conocimiento corresponde al alumno.

En esta adquisición señalamos tres etapas:

1.- aprehensión

2.- fijación

3.- integración

Utilizando el término contenido en sentido amplio, como objeto de aprendizaje, diremos que el sujeto: Aprehende un contenido cuando reconoce su significado; fija el contenido, cuando incorpora a su universo el significado en el código establecido; integra el contenido cuando establece las relaciones existentes con otros elementos de ese universo. Las tres secuencias no están aisladas, se interrelacionan y dependen mutuamente, complementándose. Sin embargo, no siempre se tiene esto en cuenta en los planteos didácticos: Se utilizan métodos interaccionistas en la fase de aprehensión y la fijación y evaluación se tornan enciclopedista. La contradicción desemboca en desinterés del alumno.

Veamos un ejemplo:

Situación: dos clases de historia en cursos paralelos Actividad de la clase: Responder en grupos un breve cuestionario y puesta en común. Ambas clases se desarrollan en forma activa e interactiva. Finalizada la hora de clase, el profesor 1 dice: "Estudien para la próxima clase" El profesor 2 entrega un texto lógico y coherente sobre el tema, donde se han deslizado un buen número de afirmaciones falsas. Solicita, como tarea, corregir los errores y transcribir el texto correctamente.

La tarea del primer profesor sólo exige memorización, la del segundo en cambio, requiere poner en práctica otras estrategias, afianza las competencias lingüísticas, y permitirá observar el grado de compromiso con la tarea y el grado de comprensión: en función de ello, pautará las actividades siguientes o la evaluación. El primer profesor podrá organizar una prueba escrita para la clase siguiente, y para el caso de fracaso masivo, podrá afirmar que los alumnos no estudian. Nosotros podemos asegurar este docente completará el programa oficial, antes que el segundo, pero ¿los alumnos realizarán los mismos aprendizajes?

El alumno es el que aprende; la fijación es un proceso individual, pero el planteo didáctico condiciona el tipo de aprendizaje y por lo tanto, debe existir coherencia en las actividades que se propongan

La selección de medios y métodos está influenciada por las políticas educativas y las corrientes pedagógicas relevantes en un determinado tiempo. En la actualidad, los criterios coinciden en promover la producción del alumno. Esta promoción requiere utilizar medios que despierten el interés y en función de ellos aparecen distintas propuestas y ofertas. Por ejemplo, los libros de texto han evolucionado, desde el libro que daba prioridad a la información, pasando por la etapa del libro de texto más el cuaderno de actividades, a los más recientes libros-cuaderno: Del máximo de contenido se pasa al mínimo y del mínimo de propuesta didáctica se pasa al máximo, se limitan los espacios de expresión del alumno y se limita la elaboración didáctica del docente. Del mismo modo, bajo el lema "una imagen vale más que mil palabras", se reemplaza la clase expositiva con una proyección de video. Entonces se requerirán actividades previas y posteriores que aseguren que el contenido ha sido internalizado, desarrollando algún proceso u operación del pensamiento, de lo contrario se corre el riesgo de generar un adiestramiento centrado en la memoria, que muchas veces disimula la ausencia de razonamiento. No se trata de descartar medios, sino de desmitificar el valor intrínseco de los mismos, teniendo en cuenta que su función es mediatizar la relación sujeto-objeto, que depende de las estrategias cognitivas que desarrolle o ponga en juego el sujeto sobre el objeto y no necesariamente del objeto en si.

Existen ciertas operaciones del pensamiento que se complementan y es necesario afianzar, sistemáticamente, para el desarrollo de la capacidad de aprender a aprender, la formación del pensamiento abstracto y la transferencia de los aprendizajes. Paralelamente, existen habilidades psicomotrices, cuya ausencia dificultad u obstruye el aprendizaje. Por ejemplo, la lectura involucra cierto entrenamiento del ojo, que incide en la velocidad y por ende, en el tiempo y el desgaste físico consecuente, que le insume al lector.

Los docentes muchas veces lamentamos la falta de espíritu critico de los alumnos, sus deficiencias en el razonamiento, la restricción de su lenguaje, su inhabilidad para el uso de libros o instrumentos, etc.. sin analizar si el tipo de experiencias de aprendizaje que proponemos desarrolla alguna de estas estrategias o silos impedimentos provienen más de los vínculos que se establecen, que de la naturaleza de los objetos de conocimiento. Raths expresa que para enseñar a pensar, es necesario proponer actividades que desarrollen los procesos que se resumen a continuación:

"Observar e informar: Describir fenómenos percibidos a través de nuestros sentidos.

Comparar: Distribuir o agrupar objetos (o ideas) conforme a ciertos principios. Ordena y da sentido a la experiencia.

Interpretar: Explicar el significado en función de las variables o principios intervinientes, de acuerdo al marco referencial.

Formular hipótesis (sacar conclusiones): Enunciar conjeturas sobre las posibles soluciones de un problema o sobre las causales de los efectos observables o acerca de presuntos comportamientos posteriores (predicciones).

Buscar hipótesis (o supuestos): Establecer explícitamente los marcos de referencia y las premisas que se consideran verdaderas cuando se sacan conclusiones, se interpreta, se toman decisiones, se formulan criticas, etc.

Resumir: Establecer en forma concisa y sin omisiones, la esencia del discurso. Requiere internalización de la estructura y síntesis de los elementos.

Reunir y Organizar datos (diseñar proyectos ): Requiere interpretación, clasificación y resumen

Formular criticas: Analizar o evaluar según ciertos principios, patrones o normas, implícitos o explícitos. Está ligada íntimamente a la formulación y búsqueda de hipótesis, la reunión y organización de datos, para la sustentación del Juicio siempre presente en la critica.

Tomar decisiones: Elegir y seleccionar entre alternativas, en forma tal que permitan resguardar los valores elegidos (implícita o explícitamente)

Aplicar principios a situaciones nuevas (resolver problemas no rutinarios): Implica percibir una estructura, relacionaría con otras ya conocidas, conjeturar y tomar decisiones.

Imaginar: Formar una idea de algo no presente. Percibir mentalmente algo no enteramente experimentado. Implica creatividad. Compartir con otro lo imaginado suele introducir mayor flexibilidad en el pensar" ,

Hay algunas actividades que se omiten en los primeros años porque se supone que los niños son demasiado pequeños y se limitan las actividades en la etapa de las operaciones concretas a la descripción de la percepción, manipulación, sin atender a las operaciones del pensamiento. Luego, a veces de un año para otro, se solicita a los alumnos realizar todas las operaciones del pensamiento, que fueron obstruidas en la etapa anterior, cuando las experiencias propuestas confundieron lógica concreta con experiencia empírica Este ejemplo muestra la diferencia: Por televisión publicitaban la consigna "leer es crecer" oiría una nena de 4 años exclamó: "¡Eso está al revés! Crecer es leer porque cuando creces sos grande, vas a la escuela y entonces lees". El asociar "crecer" sólo a lo físico es parte del razonamiento concreto, la limitación del vocablo a la experiencia empírica le hace partir de una premisa falsa, pero no obstante ello el razonamiento es válido, el silogismo seria:

• Si crece entonces se hace más grande

- Si se hace más grande entonces va a la escuela

- Si va a la escuela entonces aprende a leer

LUEGO: Si crece entonces aprende a leer. Razonamiento válido.

No es meramente anecdótico continuar la historia. A la nena se le había explicado que el mensaje era correcto porque cuando uno lee " aprende más palabras, puede decir otras cosas, etc. " . Pocos días después dijo: "estoy creciendo en patinar"

L a lógica abstracta se fundamenta sobre la lógica concreta. Las estructuras básicas se amplían.

Sin invadir el universo del niño con contenidos irrelevantes, sino por el contrario, utilizando los elementos de ese universo - para la mayoría de los cuales el niño tiene su explicación propia -, es posible poner en movimiento todas las operaciones del pensamiento. ,

Otro aspecto a tener en cuenta es la enseñanza de hábitos y métodos de estudio que requieren del alumno concentración, reflexión y disciplina. En una sociedad que ha sufrido los estragos del autoritarismo, la palabra disciplina asusta a algunos y como contrapartida se desemboca en la no-disciplina, que perjudica al individuo y en las comunidades educativas desdibuja el marco referencial de valores. Defino como disciplina individual, la organización y métodos propios, sostenidos por te voluntad,

que conducen a /a concreción cíe las tareas emprendidas ; y como disciplina institucional, el conjunto de vínculos y actitudes interpersonales, que permiten el ejercicio de la libertad individual sin perjuicio de la libertad del otro y conducen a la realización personal y al crecimiento de la comunidad.

Así, la disciplina deviene como corolario de otros valores, necesarios para el desarrollo espiritual del hombre, como son , por ejemplo:

- el respeto al otro, que permite reconocerlo como un ser trascendente y perfectible, con la misma dignidad del yo.

- la conciencia de la propia identidad, que impide el dominio externo y que anula el deseo de dominación porque identifica y respeta las otras identidades y resguarda la propia.

- la solidaridad, que implica, "estar atento al llamado del otro",

En el aspecto vincular, la persona del educador adquiere mayor trascendencia. Se pueden objetivar medios y métodos , pero el "clima" no dependerá de los valores enunciados sino de lo que ejemplifiquen los individuos y la institución, porque los valores son entes abstractos que sólo existen en las personas que los recrean.

INCURSIONANDO EN LA DIDÁCTICA

El fracaso de los alumnos en el aprendizaje de la matemática invita a la investigación de las causas. Hay muchas y buenos experiencias que dan a los docentes pautas para organizar los contenidos. A ello se le suma el esfuerzo de los buenos docentes que cada día recrean metodología y originan nuevos recursos en función de la realidad.

También, en numerosas ocasiones se ha propuestos desde los estamentos de conducción la aplicación de distintas teorías o experiencias que aparecían como una solución a todos los problemas, pero más tarde las expectativas se veían frustradas, Muchas veces de la falta de logros se lo responsabilizó al maestro

En principio hay que tener en cuenta que los resultados de una investigación psicológica o las experiencias que se llevaron a cabo, no pueden trasladarse invariantes al aula. En tanto constituyen experiencias empíricas organizadas según hipótesis previas, realizadas con un objetivo determinado - no necesariamente didáctico -, trasladadas al aula corren el riesgo de transformarse en un acto de verificación, las más de las veces reducccionista.

En lo que a matemática se refiere, a pesar de los intentos el promedio de rendimiento es del 50%, aumentando en los sectores de menores recuso.

Además, muchos alumnos que operan correctamente en la escuela primaria, fracasan a la hora de demostrar propiedades o utilizar cálculos en situaciones que exijan pensamiento reversible.

De acuerdo a la psicogénesis, las estructuras cognitivas que el individuo gesta en su desarrollo, coinciden con las estructuras matemáticas, esto es: hay coherencia interna entre la formación de las operaciones abstractas y los procesos que derivan del aprendizaje de la matemática. De allí. la importancia de incluir la enseñanza de conceptos de esta ciencia desde las primeras etapas del desarrollo. En la práctica, sin embargo, la matemática es la disciplina que produce mayores rechazos y fracasos entre los estudiantes. Esta contradicción nos lleva a analizar qué variables obstaculizan o favorecen los aprendizajes

Si partimos de que el desarrollo de las estructuras del pensamiento del individuo, está influenciado y hasta determinado por las experiencias que vivencia en cada etapa evolutiva, si las condiciones sociales y psicológicas adversas, - cuando no son extremas, como la desnutrición o ciertas patologías psicológicas-. limitan o retardan, aunque no impiden el desarrollo del individuo. es lógico pensar que una de las causas los fracasos escolares, (de la cual corresponde la responsabilidad al subsistema enseñanza) tienen más relación con la forma en que se comunican los conocimientos que con impedimentos individuales. La forma de comunicar el conocimiento, es decir, la didáctica que se utilice. promoverá o no, las construcciones internas específicas, necesarias y diferentes, que permiten establecer los significados y los significantes y las estrategias y procesos que derivan, en etapas posteriores, en la formación del pensamiento abstracto. No obstante, no pueden garantizar la realización del aprendizaje, que depende también en gran medida del compromiso del alumno con el proceso.

Al planear una didáctica de la matemática es necesario identificar la naturaleza del saber que se comunica y cómo debe ser comunicado para que atienda al nivel de desarrollo o lo promueva

l.- La naturaleza del saber matemático

a) Diferencia entre la matemática y las ciencias experimentales

La matemática es una ciencia abstracta, su objeto de estudio no pertenece al mundo material, en consecuencia, su método de estudio difiere del método de las ciencias empíricas Un conocimiento matemático está separado de los contextos materiales y aunque exprese relaciones comunes a varios contextos, no dice nada de la naturaleza de ellos Constituye, por tanto, la abstracción de las estructuras subyacentes a diversas situaciones específicamente contextualizadas.

Una hipótesis matemática es un enunciado que se asume como verdadero, del cual pueden deducirse otros a partir de un razonamiento lógico y ésta es su única prueba de validez. No se remite a la verificación empírica para sostener la verdad de sus enunciados y aún cuando ella pueda realizarse, no es prueba válida de su valor de verdad. Una hipótesis experimental, en cambio, es un resultado derivado de la observación del comportamiento de la materia, al que describe, explica o pronostica La veracidad del enunciado requiere evidencia empírica, es decir. experimentación.

Análogamente, una experiencia en una ciencia experimental constituye una construcción de elementos materiales que interactúan y producen un efecto observable, cuantificable, previsto o no en la hipótesis planteada. Pero cuando hablamos de experiencia para comunicar un saber matemático, el modelo material sólo mediatiza la construcción de una estructura abstracta La actividad de interacción del sujeto debe superar la observación cualitativa v cuantitativa o la mera manipulación de elementos concretos - pues no son ellos el objeto de la matemática -, para establecerlas relaciones estructurales que tos relacionan.

b) La matemática: una ciencia abstracta

La matemática se constituye como ciencia independiente a partir de términos primitivos que no definen y relaciones no demostradas, axiomas o postulados. Un sistema axiomático es un conjunto de enunciados, no necesariamente autoevidentes, que se asumen como ciertos y cuyo único requerimiento es que sean no contradictorios y completos. A partir de los axiomas se definen otros entes, relaciones, propiedades mediante un razonamiento

deductivo. Podríamos decir que, como ciencia de la deducción la frontera entre la matemática y la filosofía, es la ontología. La matemática prescinde de las esencias.

Ejemplifiquemos la estructura de la ciencia matemática:

Ud. seguramente ha jugado con una baraja de naipes. Pero, ¿qué es un naipe o una baraja?

Construyamos un sistema axiomático:

1} Una baraja tiene por lo menos 48 naipes o a lo sumo 52

2) Cada naipe tiene anverso y reverso

3) Los reversos de dos naipes distintos son iguales.

4) Los anversos de dos naipes quedan determinados por dos atributos 5} Dos naipes cualesquiera de la baraja tienen por lo menos una diferencia en sus anversos

En esta construcción naipe y baraja son términos primitivos, no contestamos a la pregunta qué es, no determinamos la sustancia material, sino los atributos. De esa construcción se podría deducir que no es posible distinguir un naipe de otro por el reverso, por el axioma tres. Esta afirmación, derivada lógicamente de los axiomas, serla un teorema.

Ud. tiene el concepto de baraja y le será indiferente que los naipes sean de plástico o de cartón, grandes o pequeños, circulares o rectangulares, o bien, si los dibujos tradicionales, son sustituidos por cuatro colores. Cualquiera sea la baraja, podemos jugar con ella a distintos juegos, que poseen reglas diferentes.

En cada juego los naipes tiene un valor relativo definido por las reglas. Seguramente nunca se ha preguntado acerca de la veracidad de las reglas de un juego: Sólo es necesario que atiendan a todas las posibilidades del Juego y que no se contradigan entre si. Las reglas de cualquier juego tienen la estructura de un sistema axiomático.

Un niño que puede jugar juegos estructurados, no se plantea, porque es innecesario, qué valor de verdad tienen las reglas ni cuál es la definición de naipe. Reconoce los naipes y aplicando las reglas desarrolla estrategias para ganar.

Si bien la matemática tiene pocos términos primitivos y pocos axiomas, en la práctica didáctica, muchas veces, para llegar a la abstracción de algunos conceptos matemáticos definidos a partir de axiomas o teoremas, se los induce desde la "materialización" Toda vez que se induce desde un modelo particular un concepto matemático, adquiere, en el universo del discurso, carácter de axioma.

Lo importante, al comunicar los conocimientos matemáticos es discriminar qué le es posible deducir al alumno a partir de tos conceptos que fueron incorporados por inducción. Si solamente se plantean situaciones inductivas, quizá se logre un adiestramiento para el uso mecanico de la matemática, pero se cercena parte del desarrollo del pensamiento.

2.- Enfoque didáctico

La similitud entre la estructura de la matemática y los juegos con reglas, es utilizada por Dienes para pautar principios didácticos, proponiendo las siguientes etapas: " familiarízación con tos entes (etapa del juego Ubre)

Ø percepción y aprehensión de la estructura (etapa del juego estructurado)

Ø verbalización

Ø codificación

Ø formalización

La validez de este enfoque didáctico radica en que atiende tanto a la construcción del objeto abstracto, como a la epistemología de la matemática.

Podríamos simplificar la propuesta en tres etapas ineludibles:

Aprehensión: Consiste en establecer los nexos entre el universo del alumno y la nueva estructura. "Presentar la estructura en todas sus formas perceptibles" , dice Dienes lo que implicará el reconocimiento de los elementos particulares y generales de la estructura en cada

contexto o modelo o ente. Es necesario señalar, que el modelo o ente no está limitado a objeto materia!, sino que incluye objetos abstractos construidos previamente por inducción o deducción. Verbalización: El concepto aprehendido se expresa en la lengua coloquial, esto es: se traduce en un código conocido. En este proceso se amplían las competencias lingüísticas, para facilitar la incorporación de nuevos significantes.

Formalizactón: Aislada la estructura de los contextos originarios, se codifica. La codificación es la representación de la estructura en un código metalingüístico escrito, el lenguaje matemático.

La diferenciación de estas tres etapas, no implica necesariamente distintos tiempos, pueden darse simultáneamente, dependiendo de la naturaleza y complejidad del concepto. Por ejemplo, al enseñar numeración natural, es frecuente asociar a la colección, el símbolo y nombrarlo. En cambio, si el tema es proporciones, convendrá en primer término, establecer relaciones proporcionales y no proporcionales, y formalizar el concepto una vez que la estructura haya sido internalizada y verbalizada.

3-- El lenguaje matemático

El lenguaje matemático es universal. Es un lenguaje escrito que se oraliza en la lengua materna. Expresa conceptos que pueden ser construidos lógicamente, pero, en la situación de enseñanza aprendizaje, el código no se construye, se impone, del mismo modo que es impuesta la lengua materna.

Hemos dicho que: la verbalización consiste en la comunicación del concepto aprehendido en la lengua materna. Es donde se establece la construcción de significantes para los significados aprehendidos.

La verbalización de la estructura es soporte de la etapa de formalización donde se la expresa en el lenguaje propio de la ciencia matemática. La adquisición de éste, requiere procesos y estrategias intelectuales que, a nuestro juicio, superan la mera traducción de un lenguaje a otro, es decir, es algo más que la incorporación de nuevos significantes. En efecto, el lenguaje matemático es un lenguaje escrito que se verbaliza en la lengua materna en dos sentidos:

- en la lectura literal de los signos.

- en la expresión de la estructura que involucran. Ejemplo: 2x = x + x

La lectura literal es: dos equis es igual a equis más equis. La expresión estructural podría ser: multiplicar un número por dos es igual a sumarlo dos veces.

Es necesario desde la perspectiva didáctica considerar que, abstraído el concepto, éste se constituye en objeto, con identidad propia. derivada de una estructura conceptual carente de los significados que lo originaron

La lengua materna es un sistema interpretante y el sistema interpretado es el lenguaje matemático. La interpretación, sin embargo, está limitada en las primeras etapas por las configuraciones que derivan de la lógica concreta y no por las competencias lingüísticas en la lengua materna, que deben ampliarse en la medida que se internalizan las estructuras. Nombrar correctamente los conceptos aún no formalizados, en función de su uso en aplicaciones prácticas, directas o indirectas, amplia cualitativamente el sistema interpretante y favorece la incorporación del metalenguaje matemático.

En la comunicación del saber matemático se deben atender a dos funciones:

- una instrumental, de aplicación a situaciones de la realidad.

- otra formativa de las estrategias intelectuales que conduzcan al desarrollo del pensamiento abstracto.

Así, cualquiera sea la edad del educando, se debe recorrer el camino de lo concreto a lo abstracto. Entendiendo como concreto lo que puede representarse en un modelo, sin restringir los elementos de éste a objetos materiales, sino extendiéndolo a estructuras o conceptos construidos lógicamente. El proceso deductivo debe seguir a la inducción.

La enseñanza de la matemática está dirigida a personas, y si bien pone de manifiesto los aspectos cognitivos prioritariamente, el sujeto que conoce, también posee sentimientos e imperativos físicos y psíquicos (que no se "toman vacaciones" durante el acto de conocer). Por tanto, no puede pautarse ninguna situación de aprendizaje que no conciba al ser integrado e integrándose, sin correr el riesgo de deshumanizar la acción.

ANALISIS DE MODELOS DIDACTICOS

Hemos dicho que muchos conceptos matemáticos pueden introducirse a partir de modelos empíricos y en cambio, existen otros que se derivan de construcciones lógicas previas. Pero cualquiera sea el caso, debe tenerse en cuenta la naturaleza del saber matemático y su método. Conviene señalar, por tanto, que:

- Cada concepto está ligado a otro, por lo tanto, en los planteos didácticos conviene establecer todas las relaciones posibles para mantener la coherencia lógica con los conceptos previos y con el universo del alumno.

- Existe una forma de pensamiento que se desarrolla a través de la matemática que es necesario atender, además del aspecto instrumental de aplicación a otras disciplinas que tiene esta ciencia.

- La matemática demuestra, no muestra, por lo que siempre que sea posible es necesario establecer deducciones.

- La manipulación con elementos materiales son el medio para inferir o inducir un concepto, no es un fin en si misma. El objetivo es determinar las relaciones estructurales y funcionales entre los objetos.

- El lenguaje matemático es parte del contenido, es materia de enseñanza. Se incorpora después que se ha internalizado la estructura y se la ha verbalizado en el lenguaje conocido. Requiere ampliación de las competencias lingüísticas

No se facilita el aprendizaje de la matemática desvirtuándola como ciencia, omitiendo su método u obviando el lenguaje, por el contrario, si se obra en este sentido se cometen errores conceptuales que, por contradecir la lógica interna del individuo conducen al rechazo o al olvido. Asimismo, aún cuando un concepto esté correctamente expresado, si el planteo didáctico entra en conflicto con el universo del alumno o con la lógica derivada de su etapa evolutiva, no se realizan los aprendizajes previstos.

Cuando los conceptos se enseñan mal o se plantean contradicciones internas, producen en la mente del alumno una resistencia que, se verbaliza como "no entiendo". La mente se defiende de la contradicción, generando lo que denominaríamos "anticuerpos". En el mejor de los casos el alumno olvida, en el peor, memoriza y aplica mecánicamente, sin desarrollar ningún proceso y hasta quizá obstruyendo el desarrollo posterior. ¿Tiene el derecho el docente de utilizar el tiempo y la mente de otra persona para una actividad estéril?.

Sobre los contraejemplos y propuestas

Las actividades siguientes están divididas en contraejemplos y propuestas. Un contraejemplo es un modelo que contradice una afirmación . Por ejemplo, si alguien dice: "Todos los docentes son del sexo masculino", diremos que esta afirmación es falsa porque existe Juanita, maestra de primer grado que no pertenece al sexo masculino. Es decir entonces que. cuando se desea demostrar que una afirmación general es falsa, basta con mostrar un elemento que se encuentra en el universo del discurso que no cumple la condición requerida. La contradicción, en matemática, conduce al absurdo. Si mediante un razonamiento válido se construye un absurdo, significa que las premisas que se supusieron verdaderas al iniciar el razonamiento son falsas.

Aquí he utilizado el término contraejemplo para agrupar algunos planteos didácticos que contradicen la estructura del pensamiento del niño o que, so pretexto de facilitar los aprendizajes conducen a errores conceptuales. Más allá del contenido particular de cada contraejemplo el propósito es que, a partir del análisis de ellos, cada uno genere un alerta sobre las actividades que propone, que lo lleve a reflexionar críticamente sobre la practica docente.

A continuación de los contraejemplos, se agregan algunas propuestas, no absolutamente originales y sí perfectibles, cuya pretensión es, por una parte ejemplificar el modo en que pueden confeccionarse guías de estudio o de autoaprendizaje, sin limitarse a una propuesta generalizada, para responder a las características del grupo. Por otra parte, mostrar que es posible, muchas veces sin mayores costos, mejorar la calidad didáctica.

La construcción de guía de autoaprendizaje o de estudio amplía el espectro de las operaciones del pensamiento que el alumno debe realizar en el aula, favorece el uso de bibliografía más amplia y permite utilizar la propia realidad como punto de partida.

Si la tarea se realiza institucionalmente, con el trabajo compartido de los docentes, entonces puede darse continuidad al proceso, que será de mayor calidad.

CONTRAEJEMPLOS

1.- SOBRE CONJUNTOS

La Teoría de conjunto incorporada a los currículos alrededor de 1967 no cumplió en muchos casos la función de integrar conceptos de distintas estructuras, facilitar la comprensión de las relaciones lógicas, etc. Y muchas veces no pasó de ser una unidad más, aislada del resto. Las contradicciones que muchas veces surgen del lenguaje, más tarde dificultan el aprendizaje. Entonces, en lugar de fijar estructuras que luego puedan expresarse en diversos modelos, se fijan errores.

A) Uno de los primeros temas que se presentan al iniciar el tema de conjuntos, es expresarlos por extensión y comprensión. Recordemos que expresar un conjunto por extensión implica nombrar todos los elementos. Nombrarlo por comprensión significa determinar una propiedad que defina unívocamente a todos y cada uno de los elementos.

Aparecen en algunos textos situaciones como la siguiente:

Se desea expresar por comprensión el conjunto de las vocales y se escribe erróneamente:

Según este supuesto, el conjunto:

Verificaría que H = A

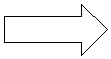
Pero podemos pensar en otro conjunto M formado sólo por la palabra "s".. Este conjunto expresado por extensión, es decir nombrando todos los elementos se escribiría igual que A

Si A es lo mismo que M , estamos diciendo que un conjunto de 5 elementos se puede escribir como uno de un elemento. Esto es un absurdo. En matemática el absurdo es error Quizá esto no confunda a quien ya conoce el tema, pero es un error y dificulta en lugar de facilitar el aprendizaje del lenguaje matemático, que es específico y preciso.

El conjunto H expresado por comprensión es:

El conjunto A expresado por comprensión es:

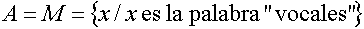
Estas expresiones "son más difíciles", si suponemos que el niño no puede entenderlo, -supuesto del que disiento, como mostraré más adelante- esperemos, no demos el contenido pero no enseñemos errores.

B) En muchos textos para los primeros ciclos aparecen situaciones como la siguiente:

Nadie duda que tres más dos es igual a cinco, pero este tipo de imagen visual, tiene varios errores:

Para el niño que se inicia en la numeración, en la etapa de las operaciones concretas, el número está ligado a los objetos que cuenta.

Aquí el niño lee tres árboles más dos gatos es igual a cinco .....¿?

Se le está pidiendo que eleve árbol y gato a la categoría de elemento, y luego sume.

A) Se está utilizando un caso particular de unión para definir la suma.

En efecto, el número de elementos (cardinal) de la unión de dos conjuntos no siempre es igual a la suma de los cardinales de los conjuntos. Para que ello ocurra, los conjuntos no deben tener elementos en común deben ser disjuntos.

B) Si estamos proponiendo al niño que sume árboles y gatos no nos asombremos luego, cuando sume centímetros y metros o cuando se le transforme en jeroglífico egipcio el tema de polinomios.

2:- SOBRE GEOMETRÍA

A) Se propone a los alumnos construir varillas de cartón con sujetadores en las puntas que permitan movilidad

Los alumnos toman la figura 1 y luego la "transforman" en la figura 2

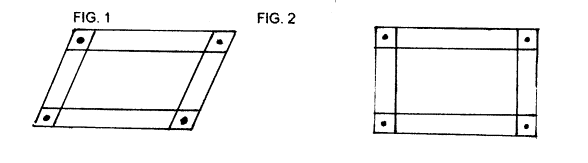
Este es un caso en el que se pretende inducir conceptos a partir de manipulaciones . Pero, ¿qué se infiere?

¿Se "genera" el rectángulo de un paralelogramo no rectángulo?

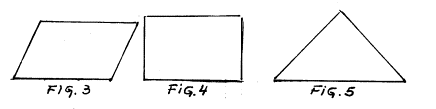
Veamos las figuras 3 y 4 tienen el mismo perímetro, pero tienen distintas áreas, ángulos}. No son congruentes, ni semejantes ni equivalentes desde el punto de vista métrico

De la igualdad del perímetro no se deduce ninguna propiedad métrica. La figura 5 tiene el mismo perímetro que las figuras 2 y 3

Para los conceptos de geometría es más fácil encontrar modelos que para otros conceptos de aritmética o álgebra, por eso el riesgo de la manipulación no estructurada es mayor. Las manipulaciones deben conducir a establecer las estructuras, para inferir generalizaciones correctas.

En geometría se debe tener en cuenta que el niño accede intuitivamente a alguna nociones topológicas: Reconoce interior y exterior, conexidad. Un cuadrado y un círculo son figuras topológicamente equivalentes, se las puede utilizar indistintamente para reconocer interior y exterior, pero desde el punto de vista métrico

La secuencia temática de la geometría podría ser:

Primero distinguir regiones, luego reconocer figuras, nombrarlas y dibujarlas, más tarde medir segmentos, áreas, ángulos. Un niño de diez años podrá trabajar mejor con las propiedades métricas si ya se ha familiarizado con las formas y nombres de las figuras.

"Es muy pequeño para usar el compás, la escuadra, para aprender tantos nombres..." Frases que oímos muchas veces.

El prejuicio sobre el niño muchas veces paraliza la acción. Para quienes quieran superar este prejuicio, he aquí una anécdota:

Hace como quince años estando en un campo vi a un grupo de niños que se entretenía construyendo plegados con papel, que según me dijeron la maestra les enseñaba. Les pedí que me enseñaran algunos de los plegados y cual fue mi sorpresa cuando una nena de ocho años me dijo: " Primero lo doblás por la mediana". Después que me explicaron qué era la mediana, le dije dibujando un cuadrado en la tierra, " Esa mediana no se puede dibujar acá, porque la tierra no se puede doblar." Uno de los chicos tomó un papel, marcó los extremos del cuadrado, lo dobló, volvió al piso y me dijo: " Se hace así". Esa maestra que nunca conocí, además de desarrollar las motricidades finas mediante el plegado, ampliaba el vocabulario de los alumnos mientras introducía correctamente algunos conceptos.

Es necesario agregar que en las manipulaciones del tipo de las varillas subyace una interpretación errónea del concepto de movimientos en el plano

Los movimientos son funciones del plano en sí mismo que conservan la pertenencia, el orden la convexidad, la conexidad el paralelismo y la congruencia.

Lo que no debe hacerse es confundir movimiento físico con movimiento en matemática.

Diferenciemos los conceptos:

Tome una plancha de plastilina y realice todas las transformaciones planas que desee sin agujerearla. Ud. realizó movimientos físicos, pero las transformaciones que obtuvo son topológicas.

Ahora dibuje una figura cualquiera en una hoja, cálquela y cópiela en cualquier parte de la misma hoja. En este caso, también ha realizado movimientos físicos pero como la figura inicial y final, al superponerse coinciden diremos que se corresponden en un movimiento (en el sentido de la definición matemática.) Son movimientos la traslación, la rotación, las simetrías central y axial.

3.- SOBRE FRACCIONES

3.1.- En una circular de apoyo para el maestro de ciclo primario decía

" Pensemos en una pastilla de jabón que materializaremos en una hoja de papel. Cortamos la hoja por la mitad: Tenemos dos medios. Tomamos un medio y los dividimos por la mitad, tenemos un cuarto.

Escribimos un medio POR un medio igual a un cuarto:

......"

Analicemos esta propuesta:

i) el niño al manipular ha "dividido" dos veces la hoja y cómo solía ocurrir con los naturales, ha obtenido una porción menor. Pero a "esto" la maestra lo llama multiplicación. Conclusión: las fracciones son raras

ii) ¿Cuál es el sentido de "materializar" el jabón"? La frase en sí misma es un absurdo. La representación de un objeto por otro que hace las veces de, nos remite al juego simbólico etapa ya superada por el niño de cuarto grado a quien iba dirigida esta actividad.

iii) Con el objeto de precisar el lenguaje, le pedimos a un grupo de niños qué explicaran o dibujaran qué entendían por "pastilla de Jabón". Los dibujos y las expresiones nos remitían a círculos pequeños, otros afirmaban que no existía tal cosa. Esto nos remite a las configuraciones que implica la lengua materna, en nuestro medio al jabón sólido se lo denomina "pan de jabón" la palabra pastilla se utiliza para las golosinas o los medicamentos. La lengua materna, como sistema interpretante debe enriquecerse y producir que las configuraciones que se generen tengan relación con el concepto a incorporar

iv) Algo positivo de esta actividad es escribir en lenguaje coloquial la expresión antes de escribirla en lenguaje simbólico.

3.2.- En el Manual Santillana Bonaerense de 6to. Grado (1993) pág. 358, sobre la división de fracciones, dice:

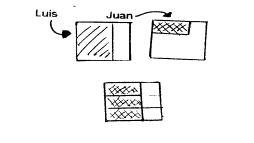
"Luis y Juan tienen dos parcelas iguales. Luis tiene sembrados 2/3 de su parcela y Juan tiene sembrados 2/9 de la suya. ¿Cuántas veces cabe la parte sembrada de Juan en la de Luis?

Lo que hay que averiguar es cuantas veces está contenido 2/9 en 2/3

Observa que en la figura 2/9 está contenido 3 veces en 2/3

Observa que:

......... " Luego el texto continúa enunciando la regla para dividir fracciones

Analicemos la actividad:

Al niño se le pide que "observe", y en estas observaciones verá que 3 es mayor que ambas fracciones, por primera vez el resultado de una división le da mayor que el dividendo y el divisor.

De todos modos podrá comprender que el 3 indica las veces en que una fracción está contenida en otra. Pero, ¿ podrá generalizar esta interpretación? . Veamos que ocurre si parodiando el problema planteado decimos que: Luis sembró un medio de su parcela y Juan un tercio. El resultado de la división es tres medios

¿Significa esto que 1/3 cabe 3/2 veces en un medio? En realidad en la parcela de Luis entran tres mitades de lo que sembró Juan..

Resulta obvio que este planteo es sumamente complicado para un niño de 10 años. Además, ¿qué configuraciones plantea la palabra "cabe" en el niño a la que va dirigida la propuesta? Supongamos que ha trabajado con múltiplos y submúltiplos y ha utilizado el cociente exacto para definirlos, no utilizó el mismo esquema de pensamiento que propone este "cabe". Desde el punto de vista conceptual este planteo didáctico es incorrecto, aunque no haya error en los resultados.

En este planteo se utiliza el concepto de relación entre dos números para definir el cociente de fracciones. Una relación se define como el cociente de dos números cualesquiera (naturales, enteros, racionales ,irracionales). Al definir relación se supone que ya está definida la división en cada conjunto numérico. El concepto de relación ligado al de proporcionalidad se deduce , no se impone. Una fracción puede pensarse como la relación (cociente) entre dos números entero, constituiría un caso particular de relación

El cociente de fracciones es uno de los temas más útiles para iniciar al niño en definiciones construidas a partir de otros conceptos matemáticos.

La suma de fracciones y el producto de una fracción por un número entero, pueden concretizarse con modelos materiales. En una segunda instancia conviene representar fracciones en la recta numérica. Sobre la recta numérica se puede trabajar con el producto de una fracción por un número entero y luego con la división de la fracción por un número entero. El producto entre dos fracciones se puede presentar primero con ejercicios y problemas que exijan que el niño multiplique y divida, procurando que los primeros ejemplos den resultado entero Luego, se define la multiplicación como simplificación de escritura :

De aquí al concepto de inverso multiplicativo.

Afianzadas estas operaciones, internalizados los gráficos el cociente de fracciones se deduce a partir de la definición de inverso multiplicativo. Este planteo no debe estar en los primeros años. El niño primero tiene que familiarizase e internalizar que la fracción es un número. Pero, volviendo a las premisas planteadas en este trabajo, es preferible esperar y no enseñar mal los conceptos.

PROPUESTAS

Estas propuestas no tienen la pretensión de ser la panacea, sin duda son perfectibles, pero si han sido utilizadas con excelentes logros. Los distintos tipos de actividades que se proponen tienen algunas características:

Ø afianzar la comunicación de resultados

Ø construir los conceptos

Ø utilizar el material concreto dentro de una estructura.

Ø el uso de diagramas de flujo para construir los conceptos o clasificar entes por sus atributos. Recorriendo el diagrama en sentido inverso se construye la definición

Ø Uso de cuadros y tablas de doble entrada, este tipo de actividad implica resumen, por lo que el alumno deberá haber realizado un análisis del tema. Comunicar los cuadros construidos favorece la traducción de un lenguaje a otro. Esta actividad como así también la de pedir al alumno que confeccione grafigramas, sopa de letras, crucigramas para luego intercambiar con sus compañeros suelen ser útiles en la etapa de fijación.

Ø Construcción de proposiciones falsas y verdaderas : reconocer el valor de verdad de afirmaciones conduce a reafirmar clasificaciones y a distinguir ambigüedades. Si, en una segunda instancia se le pide al alumno que construya y comparta este tipo de afirmaciones se afianza la comprensión y el uso del lenguaje. En el intercambio la defensa de la falsedad o veracidad de una proposición, cuando contiene ambigüedades, por ejemplo, favorece la comunicación, la racionalidad en los juicios, la precisión del lenguaje y permite establecer los implícitos del discurso

Se proponen entonces, guías de autoaprendizaje que el docente puede confeccionar y reemplazar la exposición del tema. En las guías de autoaprendizaje el alumno construye los conceptos; requieren lectura comprensiva, análisis del contenido en función del concepto a construir. Es conveniente utilizarlas como trabajo grupal, con un máximo de tres alumnos por grupo. No se supone que puedan desarrollarse en una sola hora de clase, es preferible que los temas sean abarcativos y el tiempo debe pautarse según la actividad y el diagnóstico previo hecho sobre el grupo con el que se trabaja.

El trabajo docente aquí es acompañar el análisis , sin caer en la tentación de dar la explicación cuando surge la primera dificultad, y luego, antes de evaluar los resultados en una puesta en común o exposición oral, si es necesario, arribar a las conclusiones, o acotar el universo del discurso, supuestos implícitos y enseñar aquello que el grupo no pudo aprender por sí sólo. Esta actividad del docente, que cierra de alguna manera el trabajo grupal, permite evaluar no sólo los aprendizajes de los alumnos, sino advertir los diferencias entre éstos y a través de ellos modificar y enriquecer la propuesta didáctica presentada.

GUÍAS DE AUTOAPRENDIZAJE

1.-TRIÁNGULOS

Nos proponemos:

¨ Clasificar triángulos según la medida de sus lados

¨ Construir definiciones a partir de un diagrama de flujo

¨ Traducir en acciones consignas escritas

¨ Hallar intersección de conjuntos determinados por extensión

¨ Decidir el valor de verdad de proposiciones

¨ Comunicar nuestras conclusiones

ACTIVIDADES

Realiza las siguientes actividades y luego compara tus respuestas con las de tus compañeros

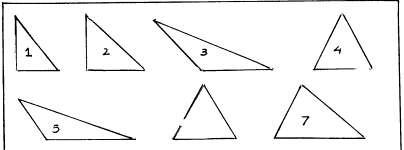
1) Calca y luego recorta los siguientes triángulos

ATENCIÓN: cuando te refieras en forma escrita a estos triángulos, escribirás el número con un pequeño triángulo arriba, y leerás triángulo uno o triángulo 2, etc.

2) haz entrar los triángulos, uno por uno en el diagrama de flujo y luego completa los conjuntos A y B

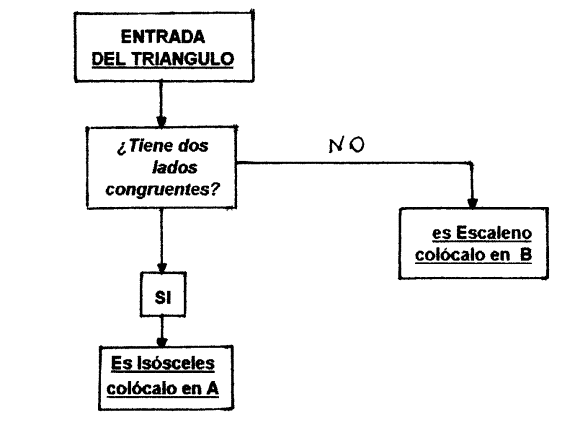
Recorre el diagrama en sentido inverso y completa:

Los triángulos isósceles tienen..............................................................................................................

Los triángulos escalenos no tienen.......................................................................................................

O sea que los tres lados son distintos

3.- Repite el procedimiento del punto 2, con el siguiente diagrama:

,

Los tri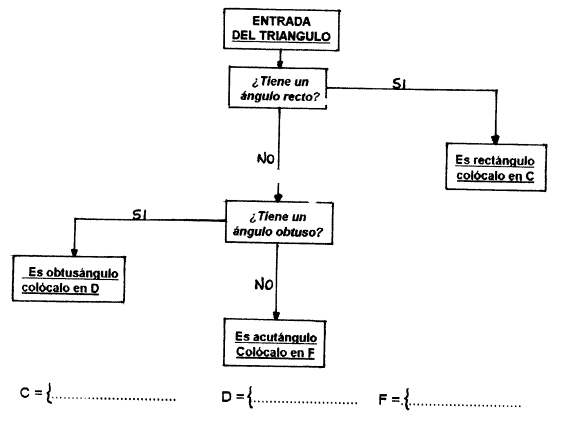
ángulos rectángulos tienen un.....................................................................................................

Los triángulos obtusángulos tienen un..................................................................................................

Los triángulos acutángulos no tienen ningún ángulo.....................ni ninguno.................es decir sus tres ángulos ........................

4.-¿ Hay algún triángulos que tenga los tres lados iguales? ¡Cuál?........

¿Cómo son sus ángulos?

Este triángulo se llama equilátero

El triángulo equilátero es el que...........................................................................................................

5.- Expresa por extensión los siguientes conjuntos (RECUERDA QUE PARA HALLAR LA INTERSECCIÓN DE DOS CONJUNTOS HAY QUE DETERMINAR LOS ELEMENTOS COMUNES)

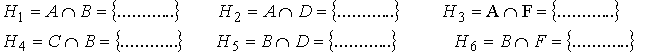
6.-Teniendo en cuenta tus respuestas del punto 5, completa el cuadro:

El Triángulo	Pertenece al conjunto	Luego es:
1	H1
2		ESCALENO RECTÁNGULO
3
4
5
6
7

7.- Coloca verdadero (V) o falso según corresponda

El triángulo equilátero tiene tres ángulos distintos

Los triángulos rectángulos son siempre isósceles

Puede existir un triángulo que sea a la vez escaleno o isósceles

Un triángulo escaleno puede ser obtusángulo

8.- Construye una evaluación: En una hoja aparte construye dos triángulos cualesquiera y tres proposiciones como las del ejercicio 7. Luego entregarás la hoja a tu compañero y recibirás la suya. Deberás clasificar los triángulos que construyó tu compañero y decidir si las proposiciones son verdaderas o falsas. Una vez concluido el trabajo, intercambiarán las hojas y corregirán los resultados. Al finalizar entregarán la evaluación al profesor. Es necesario que pongas el máximo de prolijidad al confeccionar tu prueba para que tu compañero no tenga problemas de interpretación, ya que no podrá consultarte durante el ejercicio.

2.- CONJUNTOS

Esta guía se presenta en forma parcial, se inicia con inducción del concepto de conjunto, elemento, pertenencia, expresión por extensión, cardinal, Conjunto de números naturales, orden en el conjunto de números naturales (N) y conjunto de números naturales con el cero (N₀)

...........

3) Hasta ahora hemos expresado los conjuntos por extensión, es decir, nombrando todos y cada uno de los elementos. Trataremos ahora de encontrar otra forma de escribir los conjuntos también en lenguaje simbólico.

Considera la siguiente oración incompleta

"....... es una vocal"

¿Cuántas oraciones verdaderas podemos obtener de esa oración incompleta?........

Escribe por extensión el conjunto, que llamaremos A, formado por todas las letras que, al reemplazar los puntos suspensivos hacen una oración verdadera.

A = {

En matemática

Ø a las oraciones incompletas se las llama expresiones proposicionales

Ø en lugar de puntos suspensivos se utilizan otras letras que se llaman variables ( x,y,z )

o sea que " ....... es una vocal" en leguaje matemático se escribe "x es una vocal"

Recordar: leemos equis pero pensamos en los puntos suspensivos. Aquí la equis es una variable

............

5) Utilizando expresiones proposicionales definiremos conjuntos por COMPRENSIÓN.

Relee el primer ejemplo de las vocales, que has escrito por extensión, por comprensión:

Ø se escribe

Ø se lee: A es el conjunto formado por todos los x tales que x es una vocal

Ø significa: que es el conjunto formado por todos los valores que hacen verdadera la expresión proposicional " x es una vocal"

..................

7) ¿Cómo hallamos los elementos de un conjunto que está expresado por comprensión?

Se lee:........................................................................................................................................................

Significa:...............................................................................................................................................

Buscamos todos los valores que hacen verdadera la expresión proposicional, que en este caso por ser una desigualdad se llama INECUACIÓN.

Recuerda que el primer elemento de N es el 1, entonces el conjunto B tiene 3 elementos, o sea

B = ...............

2.- NUMEROS RACIONALES

En esta actividad los alumnos de 7mo preparan el material para los chicos de tercero. Se puede también hacer la experiencia de que sean los alumnos de 7mo quienes realicen la segunda parte de la actividad con los más chiquitos.

No se ha desarrollado extensamente la guía sino los puntos más sobresalientes

Actividad 1 : (7mo)

Prepararemos las fichas para un juego de fracciones que compartiremos con nuestros compañeros de tercer grado

Materiales:

Cartulina u hoja canson nro. 3 de colores: blanco, negro, celeste, amarillo, rojo y verde.

A) Cortar rectángulos de cartulina de largo entre 20 y 23 cm de altura. ( para cinco equipos de juegos de fichas)

B) Dividir cada rectángulo en 5 tiras de tres cm de alto cada una. Estas tiras deberán dividirse en partes iguales, con el método indicado en el punto siguiente.

La cantidad de partes es la siguiente:

La tira blanca no se divide, la amarilla se divide en dos partes, la verde en tres, la celeste en 4 la roja en 6, la negra en 12.

Las particiones en 2, 4 y 8 partes, son fáciles, pero para mayor exactitud sobre todo con los tercios se procede así

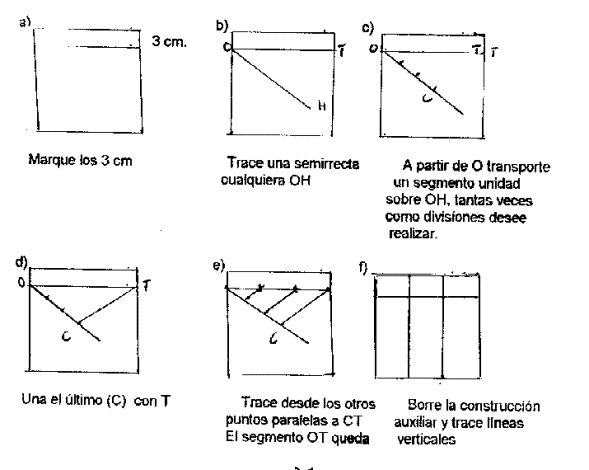
C ) Arme los juegos de fichas. Cada juego contiene: 1 blanca dos amarillas tres verdes, 4 celestes,6 rojas y 12 negras Las fichas se entregan marcadas sin recortar

ACTIVIDAD 2: (3ER. GRADO)

Cada alumno tiene un juego de fichas. Trabajan en grupos de tres

A) Nos familiarizamos con nuestras fichas y le ponemos nombr

i) Recorta las fichas por las líneas. La blanca no tiene líneas para cortar

ii) Llamaremos 1 al largo de la dicha blanca

BLANCA 1

iii) ¿Cuántas fichas amarillas cubren la ficha blanca? ¿En cuántas partes se divide el largo de la ficha blanca para tener el largo de la ficha amarilla?.....

El largo de la ficha amarilla es igual al largo de la ficha blanca dividido dos

Escribimos en lenguaje matemático la oración anterior:

La línea la leemos "dividido"

Como la ficha blanca se llama 1, es

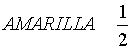
La amarilla se llama "un medio"

Escribe en cada ficha amarilla su nombre en lenguaje simbólico

................................................................................................................................................................ Se repite el procedimiento para el resto de las fracciones. Es importante que finalizada esta parte de la actividad los niños nombren indistintamente el color o la fracción que corresponde.

iv) Jugando con las fichas

Número de jugadores 2.

Colocar en una bolsita dos juegos de fichas con excepción de la blanca que la conserva cada jugador como referencia

En la primera vuelta cada jugador saca tres fichas de la bolsa. En las vueltas siguientes saca dos y devuelve una.

El objetivo del juego es obtener filas del mismo largo que la blanca con fichas del mismo o distinto color. Cuando recoge sus fichas en cada turno, el jugador debe seleccionar una para ir completando una fila o para comenzar otra.

Toda vez que se completa 1 se obtiene un punto

Cuando no hay más fichas se realiza el conteo. Un punto por cada fila formada.

Con las fichas de las filas no completadas, cada jugador arma una fila larga. Superpone la blanca. Resta 1 punto por cada vez que la blanca cabe en la fila .

V) Comparando fichas

Toma una ficha blanca y una amarilla. Superpone una sobre otra:

La ficha......................es mayor que . la ficha ........................

Escribimos en lenguaje matemático

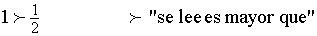
La ficha amarilla es menor que la ficha blanca

En lenguaje matemático

...................................................

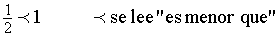
Se establecen relaciones entre varias fichas

.................................................................................

Compara tus fichas y coloca en el casillero verdadero (V) o falso (F)

Compara tus fichas u coloca el signo que corresponda

....................................................................................

Se pueden repetir estas actividades con fichas de otras formas circulares, octogonales, para que la forma y el color pasen a segundo plano.

vi) Sumando fichas:

A una ficha amarilla le agregamos dos fichas amarillas más, obtenemos tres amarillas.

En lenguaje matemático se escribe

El signo + , se lee y significa agregar

...........................................

Se continúa con sumas sencillas que se pueden calcular superponiendo fichas.

En una segunda instancia , cuando se ha internalizado la estructura se puede introducir el concepto de recta numérica.

....................................................................................................................................

3 .- PROBLEMAS Y REALIDAD

Muchas veces se ha discutido acerca de que se debe trabajar con la realidad del niño, y las más de las veces esto es una limitación para los niños que tienen menos experiencias, vocabulario o estímulos. Partir de la realidad no debe significar no ampliarla con nuevas experiencias, supuesto, configuraciones. Adaptar los problemas a la realidad significa percibir el modo en que cada concepto se aplica en un determinado contexto. En la abstracción del concepto , este se libera de las particularidades, cuando se aplica las particularidades de la realidad deben considerarse.

Son dos procesos: Primero a partir de los modelos se infiere el concepto, se abstrae y luego se aplica a otros modelos

Veamos algunos ejemplos.

a) Necesito cortar 45 cuadrados de 4 cm de lado para hacer tarjetas, y las cartulinas que puedo comprar. miden 25 de largo por 30 cm de ancho ¿Cuántas cartulinas debo comprar?

Solución

Respuesta: parece que con una cartulina alcanza.

"Así que compré sólo una cartulina y sólo pude cortar 42 cuadrados y me sobró una tira que me es inservible.

La matemática no sirve para las cosas reales"

El problema está bien resuelto pero nos ha dado la relación entre el área de la cartulina y la de los cuadrados

Esto es verdadero pero también es cierto que la superficie de la cartulina no incluye esta cantidad de cuadrados enteros. Esto nos lleva a recordar que los concepto matemáticos están descontextualizados, entonces cuando se trata de encontrar una solución para aplicar a la realidad hay que tener en cuenta sobre qué conjunto numérico se trabaja y que otras propiedades o conceptos ha y que incorporar al análisis del problema.

La solución del problema sería, resuelto por regla de tres simple:

En 25 cm del largo de la cartulina caben 6,25 lados de 4cm, o sea,6 lados enteros

En

30 cm del ancho entran 7,5 lados de 4 cm. Osea, 7 lados enteros.

Total de cuadrados enteros =42

Respuesta: debo comprar dos cartulinas

b) Tengo 28 botellas para colocar en cajones cuya capacidad es de 6 botellas cada uno.

¿Cuántos cajones necesito? ¡Cuántas botellas me sobran?

Solución

Al dividir 14 por tres obtenemos cociente 4 y resto 2. Es decir que aparentemente necesitamos 4 cajones y sobrará una botella. Veamos 4 cajones con seis botellas son 24 botellas. Éstas más las dos del resto son 26 ¿dónde están las otras 2 que faltan?

Cuando se simplifica y luego se divide el resto de la división entera debe ser multiplicado por los números por los que se simplificó

3) Anécdota: " Estaba dando clase en 7mo grado de una escuela, el tema era regla de tres simple. Como no había venido la maestra de tercero, habían distribuido a los niños en las distintas aulas.

Copié en el pizarrón el siguiente problema: " 10 obreros construyen una habitación en 15 días. ¿Cuántos días tardarán 5 obreros para realizar el mismo trabajo?

El nene de tercero exclamó: "eso no se puede saber". Por supuesto, los más grandes entre risas y exclamaciones le hacían entender que esto era "la matemática de 7mo..

Finalmente, al ver que insistía le pregunté porque no se podía saber: " Puede saber más o menos, pero puede llover, o los hombres pueden ser más vagos, o también a veces no llega el material y la gente no puede trabajar".

El niño tenía razón pero ello no implica que el problema esté mal planteado, sino que no están explicitados los supuestos: en iguales condiciones que los anteriores

Establecer los implícitos del problema, implica establecer las hipótesis que condicionan una toma de decisión o una conclusión. Esto es válido, no sólo en matemática: Cuando emitimos un juicio, implícitamente expresamos nuestro universo de valores. El distinguir claramente cuál es el marco referencial sobre el cual se formula un juicio, una crítica, un pronóstico o un supuesto, favorece la racionalidad de las conclusiones

5.- INTEGRACIÓN DE ÁREAS - INTERDISCIPLINARIEDAD

En el comienzo de la civilización, cuando el hombre aún respondía a muchas respuestas con un enfoque mítico, los sabios podían poseer la totalidad de los saberes de la época. Con la adquisición de mayor conocimiento a través del tiempo, las disciplinas se independizaron.

Una de las características de las ciencias en este siglo fue la especialización, sin embargo, la misma ciencia al avanzar mostró que existen campos del conocimiento donde la línea divisoria entre las disciplinas se desdibuja y donde un estudio parcializado, desde una disciplina en particular, limita la comprensión del objeto.

La teoría mecanicista, como hemos señalado, compite con las teorías sistémicas, cuya importancia queda manifiesta especialmente en los estudios sociales y psicológicos. En estos, por ejemplo, puede observarse, que muchas veces distintas condiciones iniciales, derivan en la misma patología, esto es: iguales condiciones finales. Premisa opuesta a un concepto netamente mecanicista donde a condiciones iniciales iguales, corresponden condiciones finales iguales.

El tratamiento interdisciplinario de los contenidos de enseñanza, aparece como un valor en los enfoques educativos, por cuanto evita la taxonomización. amplia el universo del discurso y favorece la integración y transferencia de los aprendizajes. Sin embargo, en este enfoque, no deben descuidarse los procesos y métodos propios de las disciplinas que se relacionan.

El "aprender a aprender" exige que el alumno incorpore los aspectos sustantivos y metodológicos de las diversas disciplinas: Por una parte el "qué" , responde al contenido y por otra el "como" que remite a los modos de conocer ese contenido.

Las situaciones didácticas deben plantearse sobre un objeto definido y al desarrollar las actividades, los diversos medios de abordaje deben quedar explicitados.

En matemática la relación con otras asignaturas muchas veces se ha limitado a la presentación de problemas que utilizan situaciones de otras ciencias.

Las experiencias de proyectos aquí presentadas muestran que, sobre todo en los años previos a la escuela secundaria, es posible no sólo integrar sino derivar conceptos de actividades interdisciplinarias

PROYECTO 1: Magnitudes proporcionales. Proporciones

Nos Proponemos:

§ Identificar las relaciones de proporcionalidad

§ Identificar relaciones no proporcionales.

§ Medir magnitudes.

§ Comparar resultados

§ Organizar información

§ Aplicar definiciones

§ Sacar conclusiones

Actividades:

Instrucción previa: Para la organización de tu trabajo destinarás una hoja para cada actividad, a los efectos de que puedas ir agregando datos a medida que vayas ampliando tu información.

1) Sembrar una semilla (preferentemente alpiste). Medir la altura 12 días y completar el cuadro:

día	Altura
1
...
12

2.) En un recipiente cilíndrico transparente pegar logitudinalmente una tela adhesiva . marcar la base interior y poner 0. agregar sucesivamente, cantidades iguales de agua con un jeringa y marcar cada nivel hasta llenar el vaso. Medir las alturas de cada columna y completar el cuadro

Volumen (V) Cm^3	Altura(h) cm
0	0
5
...

3) Repite el procedimiento del punto 2 con un recipiente no cilíndrico

4)Colgar de un resorte o banda elástica un platillo de plástico. Colocar en el platillo, sucesivamente distintos pesos conocimos y medir el estiramiento. Completar el cuadro. ( asigna el cero al largo del resorte con el platillo)

Peso (P) gf	Estiramiento (E) cm
0	0
...

5) Pesar distintos volúmenes de agua y hacer un cuadro como los anteriores.

6) Construir rectángulos de modo que el área sea 24. Completar el cuadro

Base (b) cm	Altura (h) cm	Area=b.h Cm^2
1		24
2		24
3		24
4		24
6		24
8		24
12		24
24		24

7) Averigua el costo de una botella de un litro de aceite en el supermercado de tu barrio, el costo de una botella de litro y medio y de tres o cinco litros.. Confecciona un cuadro para cada costo

litros	costo
10		24
20		24
30		24
40		24
50		24
60		24
70		24
80		24

8) Dos hormigas están caminando. Cuando una recorre dos metros la otra recorre la mitad. Si la primera recorre tres , la otra la tercera parte y así sucesivamente

Completa el cuadro:

Hormiga 1	Hormiga 2
Espacio 1 (x) cm	Espacio 2 (y) cm
2	1/2
3	1/3
5
6
7
8	1/8
9
10

9) En un laboratorio se ha realizado un cultivo de bacterias y se observó que se duplican cada 5 segundos. Confecciona el cuadro

tiempo (T) minutos	Número de bacterias (n
0	2
5
10
15
20
25
30
35

10) Coloca un recipiente con agua fría sobre la llama de un mechero. Mide la temperatura cuando inicias el proceso, tiempo 0, y luego cada 3 minutos, cuando comience la ebullición mide la temperatura en los vapores. Mientras dura la ebullición continúa midiendo la temperatura durante quince minutos más.

Confecciona un cuadro de valores de las magnitudes medidas: tiempo y temperatura

11)En una tienda realizan un 15% de descuento por cada compra, ayuda al vendedor a completar el cuadro

Valor de la compra $	Descuento $
100	15
200
300
400
500
600
700
800

12) analiza los cuadros de las once actividades e investiga si el producto en cada fila se mantiene constante

En los cuadros que ello no ocurra , investiga si el cociente se mantiene constante.. Escribe en la tercera columna la constante.

Si has respetado la consigna, tendrás tus experiencias en hojas separadas, clasifícalas y ordénalas

1. El producto se mantiene constante , experiencias......................

2. El cociente se mantiene constante, experiencias......................

3. No hay constante.................................

13) Representa cada cuadro en un par de ejes coordenados. Compara las figuras y compara con el ordenamiento del punto anterior del punto anterior

14) La matemática define-

1 - Dos magnitudes A y B son directamente proporcionales, si el cociente A/ B se mantiene constante

2 - Dos magnitudes A y B son inversamente proporcionales si el producto A B se mantiene constante

Teniendo en cuenta estas definiciones completa-

Son magnitudes directamente proporcionales, las relacionadas en las experiencias del grupo Son inversamente proporcionales, las del grupo Las del grupo no cumplen ninguna de las dos condiciones por lo tanto, no

Observa los gráficos obtenidos-

El gráfico de dos magnitudes directamente proporcionales es ................................

El gráfico de dos magnitudes inversamente proporcionales es una hipérbola

...........................................................................................................................................................

Este proyecto se continúa por diversas vías, y queda como referencia para temas de matemática y ciencias naturales

Este proyecto es de largo plazo, ya que algunos ítems, (como el 13, por ejemplo, que requiere uso correcto de los ejes cartesianos y escalas) pueden demandar actividades de aprendizaje extra, para que luego el alumno pueda realizar sólo las experiencias

La importancia del concepto de proporcionalidad radica en su aplicación en otras ciencias y disciplinas La inducción de este concepto a partir de mediciones que se tabulan y grafican, desarrolla diversas estrategias de conocimiento y permiten familiarizarse con instrumentos y definir correctamente las magnitudes usuales, quizá no formal, pero si sistemáticamente A la vez que se incorporan algunas estructuras que luego se explicitarán. Por ejemplo, si la experiencia le ha demostrado que, al colgar un peso del resorte, este se estira hacia abajo, no habrá dificultad más adelante, cuando clasifique el peso cuerpo como una fuerza para representarlo como un vector vertical, con sentido hacia abajo

Muchas veces se subestima a los alumnos y se omite utilizar conceptos o instrumentos Las magnitudes como tiempo, peso, longitud, están incorporadas al universo del niño, en distintos grados. Omitirlos y luego imponer su formalización, obstruye la comprensión Lo mismo ocurre con el uso de instrumentos de medición y construcción (escuadra, regla, compás) donde a veces, los alumnos arrastran deficiencias psicomotrices que hubieran requerido un poco de adiestramiento en la etapa anterior, en alguna actividad no necesariamente matemática

El niño aprende a manejar su triciclo, antes de poder pronunciar correctamente la palabra y bastante tiempo antes de poder escribirla. Del mismo modo, la familiarización con conceptos e instrumentos, en abordajes graduales, sistemáticos debe preceder a la formalización

Proyecto 2: Simetría y Optica

ACTIVIDADES:

1) Coloca un espejito sobre la recta de modo que el banderín se refleje en el espejo

Observa atentamente el lugar, entro del espejo dónde se ve la imagen. Luego dibuja la imagen del banderín en la zona de la hoja que representa el interior del espejo

2) construye la imagen en un espejo de la siguiente figura. Luego coloca el espejo

3) Estos dos dibujos representan una figura y su imagen en un espejo. ¿Dónde estaba colocado el espejo?

3) En el dibujo 1 mide la distancia de la punta del banderín al eje y de este a la punta de la imagen

Repite el procedimiento con todos los vértices de la figura

¿Puedes sacar alguna conclusión? ¿Esa conclusión es válida para las otras figuras?

.............................................................................................................................................................................

Aquí este proyecto se desvía en dos áreas: En matemática para definir simetría axial, y luego aplicarla a los polígonos y derivar sus propiedades y en ciencias para estudiar las nociones básicas de óptica física

* Se agradece a la Voluntaria, de la Biblioteca Virtual Universal, Profesora María Luz Silva la autorización para la publicación del presente libro.